Random Search for Regression Tasks

Source: R/RandomSearchRegr.R

RandomSearch randomly samples a population of candidates and returns non-dominated candidates w.r.t to the objectives of MOC (Dandl et. al 2020) as counterfactuals. RandomSearch is equivalent to MOC with zero generations and the random initialization strategy.

The four objectives of MOC (Dandl et. al 2020) to are:

  1. Distance to desired_prob (classification tasks) or desired_prob (regression tasks).

  2. Dissimilarity to x_interest measured by Gower's dissimilarity measure (Gower 1971).

  3. Number of feature changes.

  4. (Weighted) sum of dissimilarities to the k nearest data points in predictor$data$X.

Details

RandomSearch is typically used as a baseline in benchmark comparisons with MOC. The total number of samples drawn is mu * n_generations. Using separate parameters mu and n_generations is only required to make certain statistics comparable with MOC (e.g. the evolution of the dominated hypervolume).

References

Dandl, S., Molnar, C., Binder, M., and Bischl, B. (2020). "Multi-Objective Counterfactual Explanations". In: Parallel Problem Solving from Nature – PPSN XVI, edited by Thomas Bäck, Mike Preuss, André Deutz, Hao Wang, Carola Doerr, Michael Emmerich, and Heike Trautmann, 448–469, Cham, Springer International Publishing, doi:10.1007/978-3-030-58112-1_31 .

Deb, K., Pratap, A., Agarwal, S., & Meyarivan, T. A. M. T. (2002). "A fast and elitist multiobjective genetic algorithm: NSGA-II". IEEE transactions on evolutionary computation, 6(2), 182-197.

Goldstein, A., Kapelner, A., Bleich, J., and Pitkin, E. (2015). "Peeking Inside the Black Box: Visualizing Statistical Learning with Plots of Individual Conditional Expectation". Journal of Computational and Graphical Statistics 24 (1): 44–65. doi:10.1080/10618600.2014.907095 .

Gower, J. C. (1971). A general coefficient of similarity and some of its properties. Biometrics, 27, 623–637.

Li, Rui, L., Emmerich, M. T. M., Eggermont, J. Bäck, T., Schütz, M., Dijkstra, J., Reiber, J. H. C. (2013). "Mixed Integer Evolution Strategies for Parameter Optimization." Evolutionary Computation 21 (1): 29–64. doi:10.1162/EVCO_a_00059 .

Active bindings

optimizer

(OptimInstanceBatchMultiCrit)
The object used for optimization.

Methods

Public methods

Inherited methods

Method new()

Create a new RandomSearchRegr object.

Usage

RandomSearchRegr$new(
  predictor,
  fixed_features = NULL,
  max_changed = NULL,
  mu = 20L,
  n_generations = 175L,
  p_use_orig = 0.5,
  k = 1L,
  weights = NULL,
  lower = NULL,
  upper = NULL,
  distance_function = "gower"
)

Arguments

predictor

(Predictor)
The object (created with iml::Predictor$new()) holding the machine learning model and the data.

fixed_features

(character() | NULL)
Names of features that are not allowed to be changed. NULL (default) allows all features to be changed.

max_changed

(integerish(1) | NULL)
Maximum number of feature changes. NULL (default) allows any number of changes.

mu

(integerish(1))
The population size. Default is 20L. The total number of random samples is set to mu * n_generations. See the Details section for further details.

n_generations

(integerish(1))
The number of generations. Default is 175L. The total number of random samples is set to mu * n_generations. See the Details section for further details.

p_use_orig

(numeric(1))
Probability with which a feature/gene is reset to its original value in x_interest after random sampling. Default is 0.5.

k

(integerish(1))
The number of data points to use for the forth objective. Default is 1L.

weights

(numeric(1) | numeric(k) | NULL)
The weights used to compute the weighted sum of dissimilarities for the forth objective. It is either a single value or a vector of length k. If it has length k, the i-th element specifies the weight of the i-th closest data point. The values should sum up to 1. NULL (default) means all data points are weighted equally.

lower

(numeric() | NULL)
Vector of minimum values for numeric features. If NULL (default), the element for each numeric feature in lower is taken as its minimum value in predictor$data$X. If not NULL, it should be named with the corresponding feature names.

upper

(numeric() | NULL)
Vector of maximum values for numeric features. If NULL (default), the element for each numeric feature in upper is taken as its maximum value in predictor$data$X. If not NULL, it should be named with the corresponding feature names.

distance_function

(function() | 'gower' | 'gower_c')
The distance function to be used in the second and fourth objective. Either the name of an already implemented distance function ('gower' or 'gower_c') or a function. If set to 'gower' (default), then Gower's distance (Gower 1971) is used; if set to 'gower_c', a C-based more efficient version of Gower's distance is used. A function must have three arguments x, y, and data and should return a double matrix with nrow(x) rows and maximum nrow(y) columns.

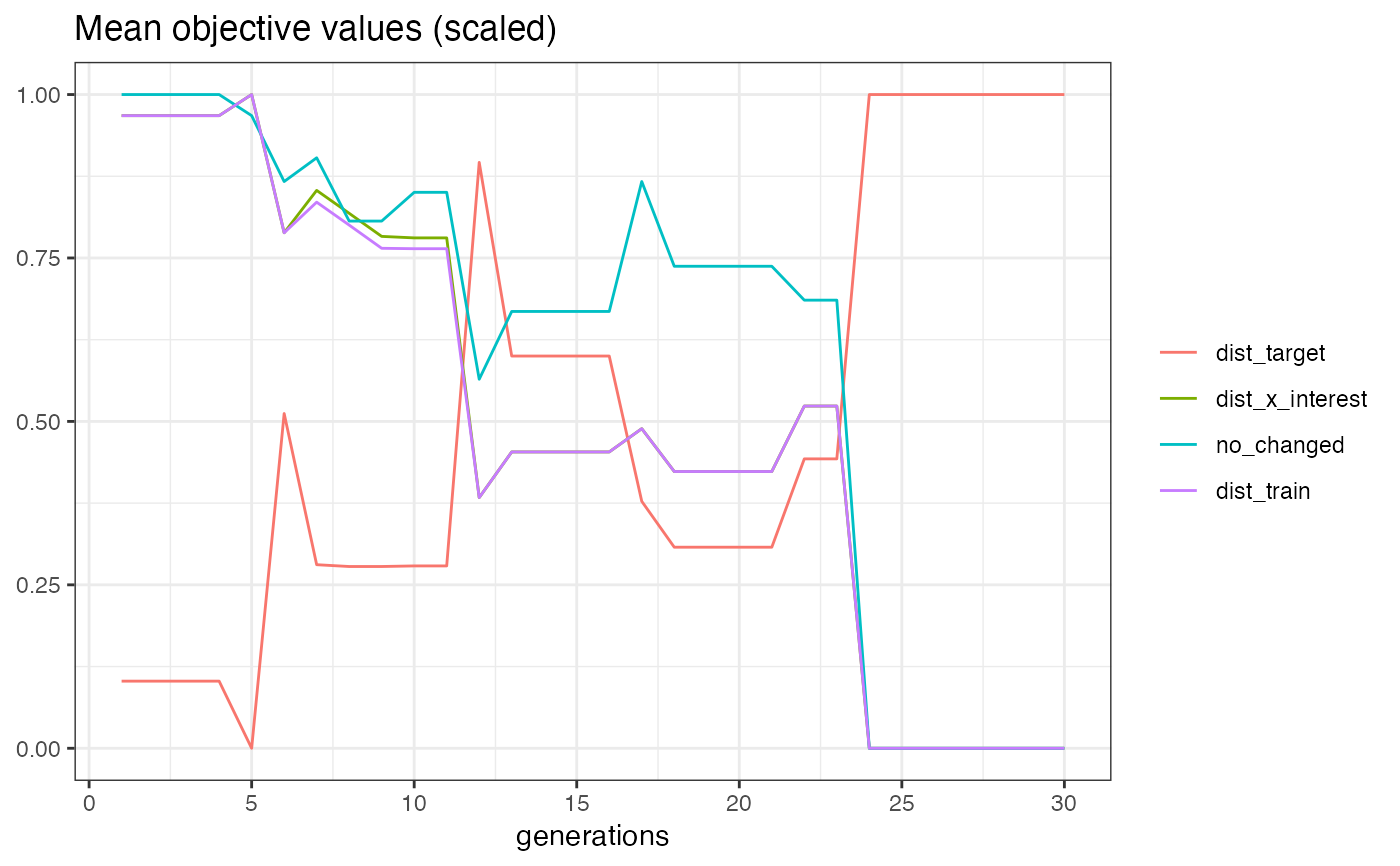
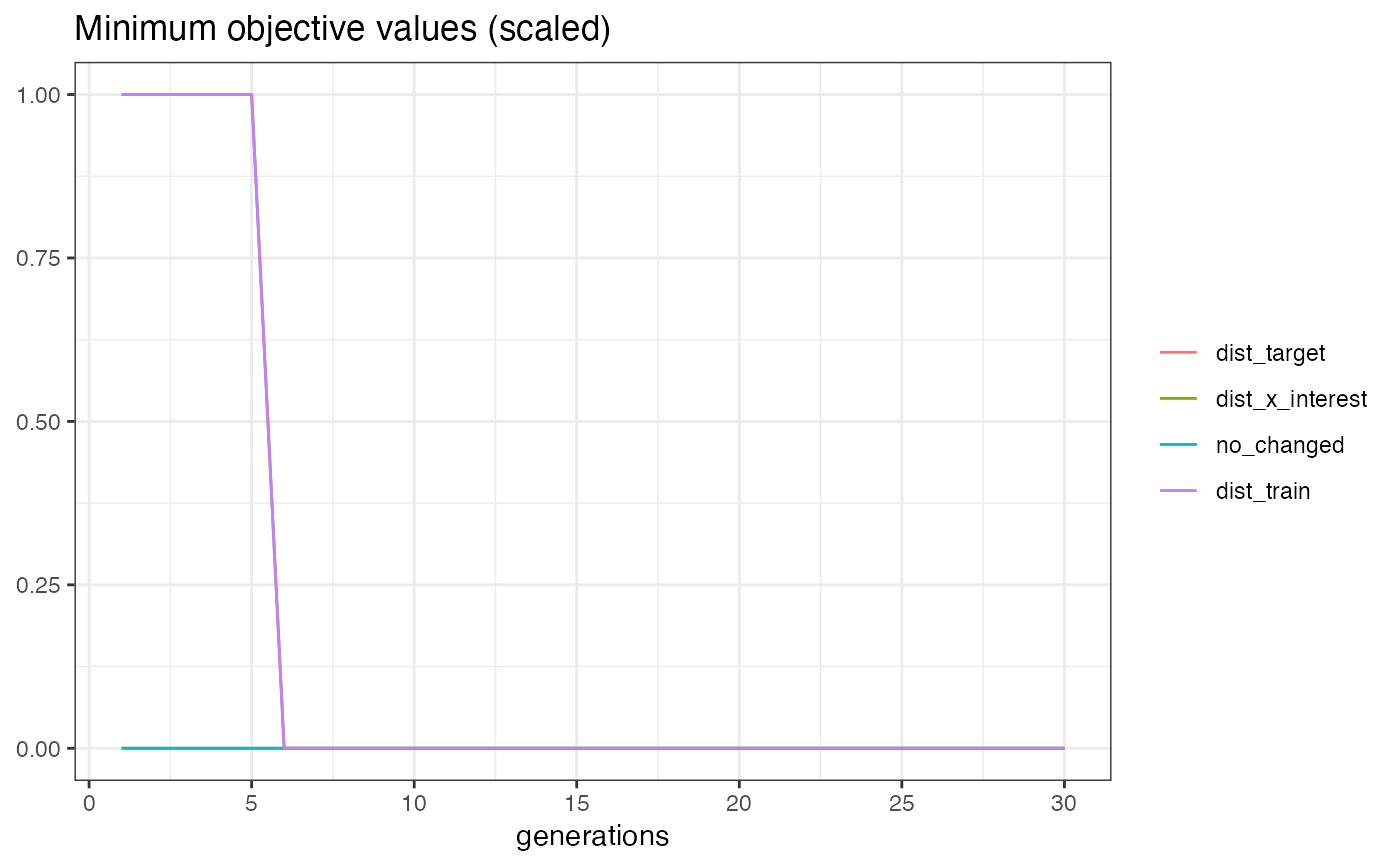
Method plot_statistics()

Plots the evolution of the mean and minimum objective values together with the dominated hypervolume over the generations. All values for a generation are computed based on all non-dominated individuals that emerged until that generation. The randomly drawn samples are therefore split into n_generations folds of size mu. This function mimics MOCs plot_statistics() method. See the Details section for further information.

Usage

RandomSearchRegr$plot_statistics(centered_obj = TRUE)

Arguments

centered_obj

(logical(1))
Should the objective values be centered? If set to FALSE, each objective value is visualized in a separate plot, since they (usually) have different scales. If set to TRUE (default), they are visualized in a single plot.

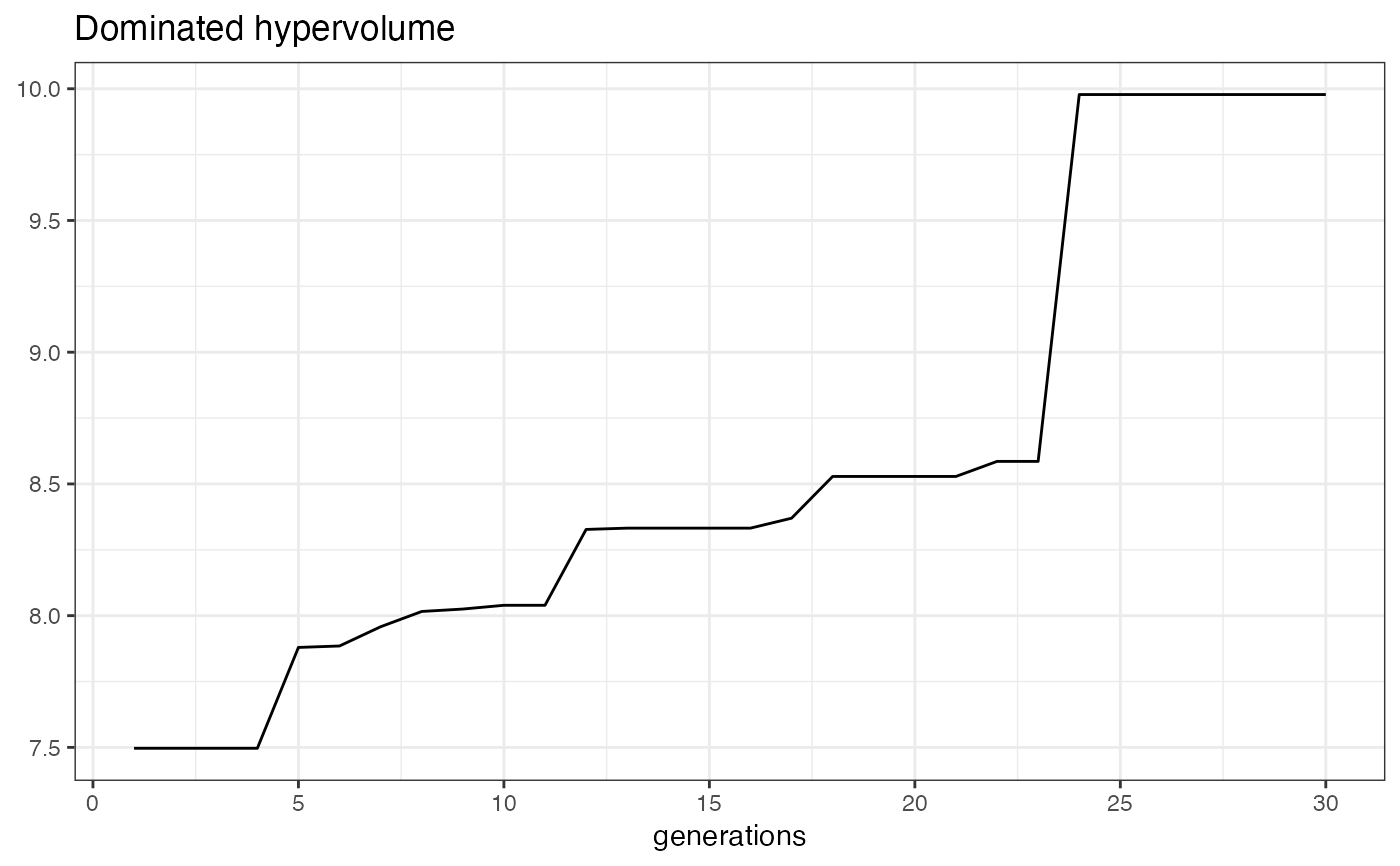
Method get_dominated_hv()

Calculates the dominated hypervolume of each generation. The randomly drawn samples are therefore split into n_generations folds of size mu. This function mimics MOCs get_dominated_hv() method. See the Details section for further information.

Usage

RandomSearchRegr$get_dominated_hv()

Returns

A data.table with the dominated hypervolume of each generation.

Method plot_search()

Visualizes two selected objective values of all emerged individuals in a scatter plot. The randomly drawn samples are therefore split into n_generations folds of size mu. This function mimics MOCs plot_search() method. See the Details section for further information.

Usage

RandomSearchRegr$plot_search(objectives = c("dist_target", "dist_x_interest"))

Arguments

objectives

(character(2))
The two objectives to be shown in the plot. Possible values are "dist_target", "dist_x_interest, "no_changed", and "dist_train".

Method clone()

The objects of this class are cloneable with this method.

Usage

RandomSearchRegr$clone(deep = FALSE)

Arguments

deep

Whether to make a deep clone.

Examples

if (require("randomForest")) {
  # Train a model
  rf = randomForest(mpg ~ ., data = mtcars)
  # Create a predictor object
  predictor = iml::Predictor$new(rf)
  # Find counterfactuals for x_interest
  rs_regr = RandomSearchRegr$new(predictor, n_generations = 30L)
  cfactuals = rs_regr$find_counterfactuals(x_interest = mtcars[1L, ], desired_outcome = c(22, 26))
  # Print the counterfactuals
  cfactuals$data
  # Plot evolution of hypervolume and mean and minimum objective values 
  rs_regr$plot_statistics()
}
#> [[1]]

#> 
#> [[2]]

#> 
#> [[3]]

#>